Data Manifold Convolution: a technique for computing similarity between point clouds

Data Manifold Convolution

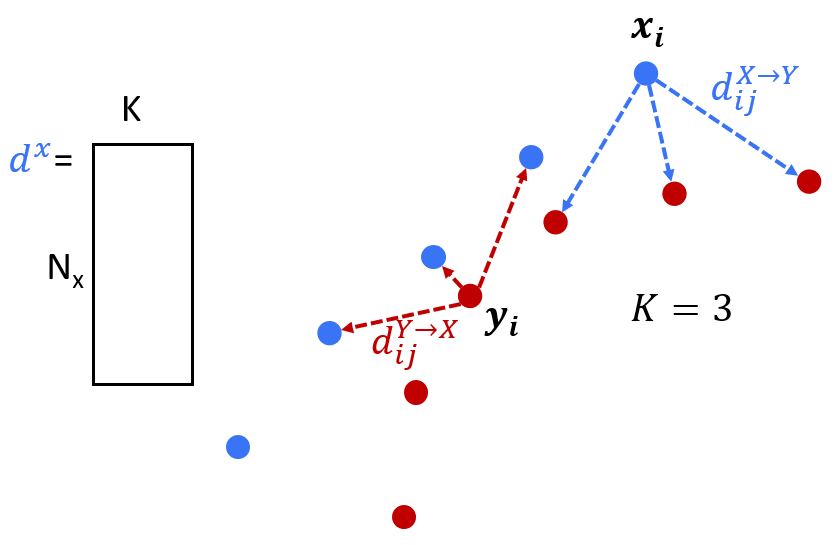
My Data Manifold Convolution repository includes matlab functions (DMC_symmetric.m, DMC_asymmetric.m) which implement an operation I developed called data manifold convolution (DMC). DMC takes two sets of vectors, in a space of arbitrary dimensionality, and one parameter k, and computes a metric of their effective “overlap.” Similar to ordinary convolution, DMC will output a higher value if the two sets of points coincide in their spatial distributions. Specifically, for two sets X and Y, DMC looks at the k-nearest neighbors of each point of X in set Y, and vice versa. It then averages the similarities between the points in X and its K-nearest neighbors in Y and vsv. The code here uses a radial basis function kernel/normal distribution-based similarity metric between pairs of points.

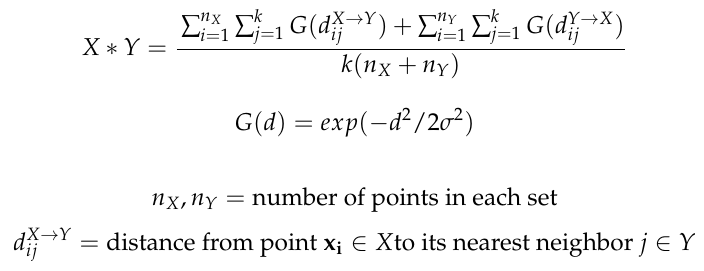
Several variants of this function are possible. DMC_asymmetric.m computes a convolution value from the ‘perspective’ of only one of the sets.

Example in 2D

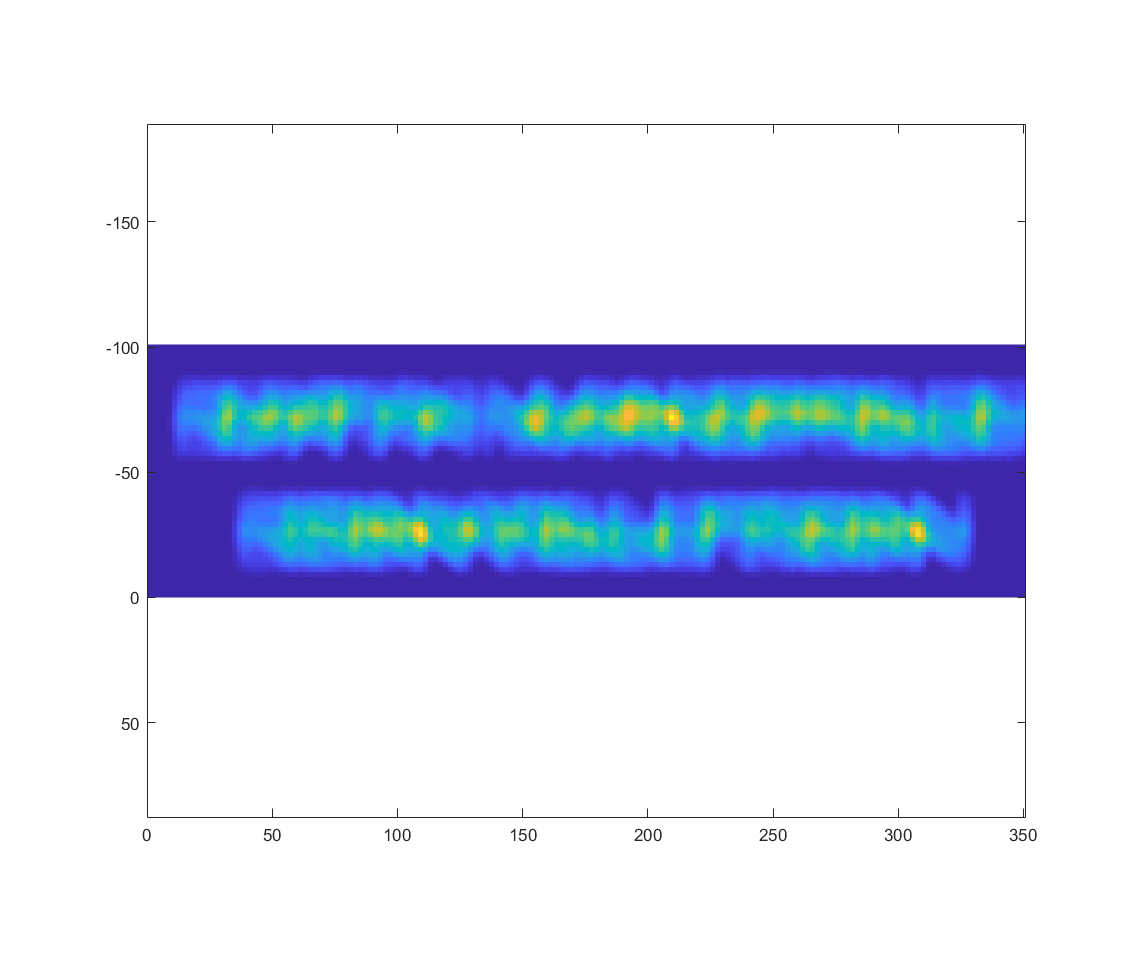
sample data includes a sample convolution kernel shaped like the letter N and a set of points shaped like some words. In Explore_DMC_parameters.m you can test out DMC by convolving the “N” over the entire data set. Spoiler alert:

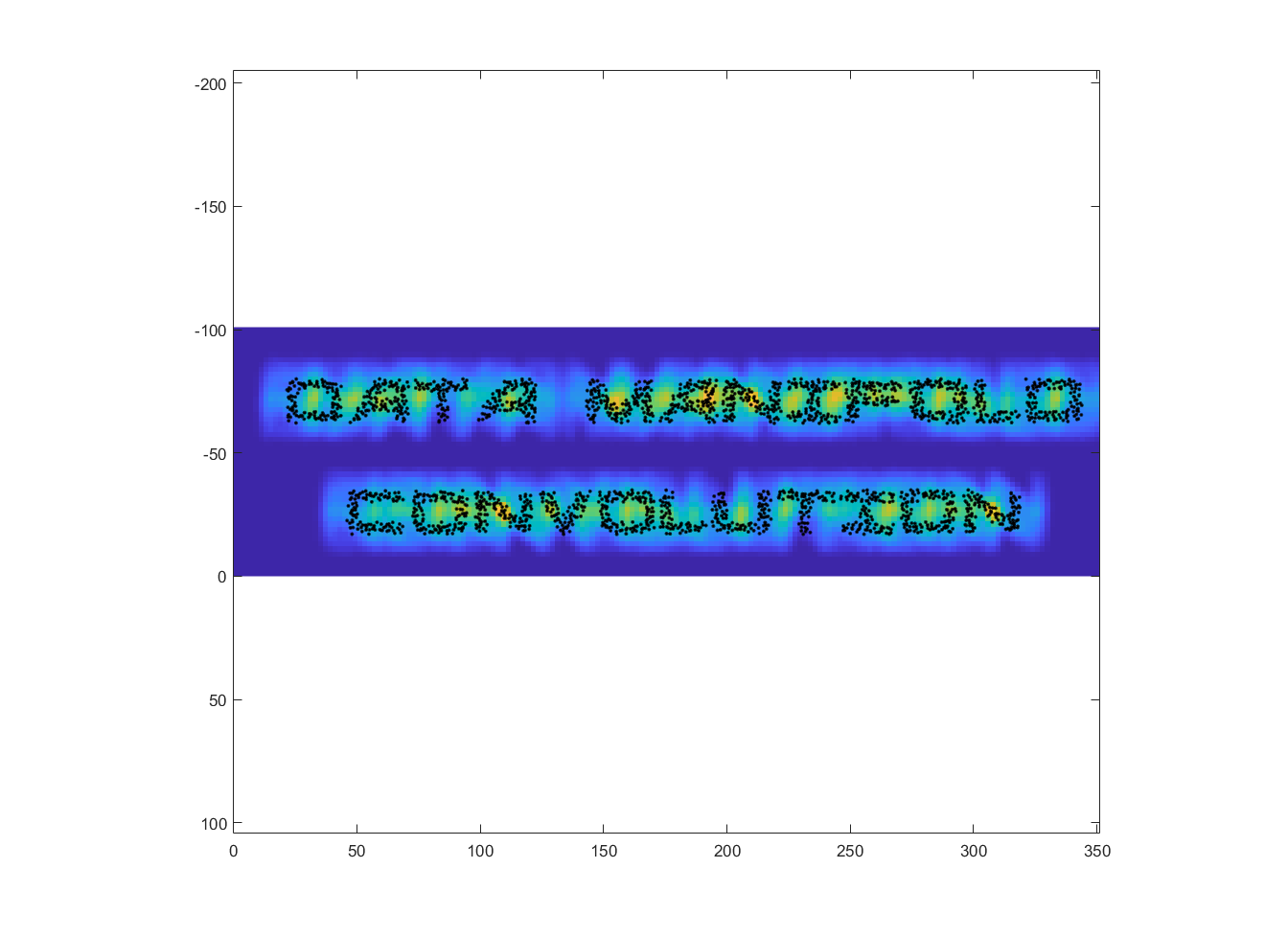Yellow indicates higher values of the convolution. There is a small sharp peak at the center of each N. It’s typical, even in ordinary image convolution, for this sharp peak to happen when a near perfect overlap is found.